Gravity remains a challengeThe Extreme Corners of Quantum Gravity

1 October 2025

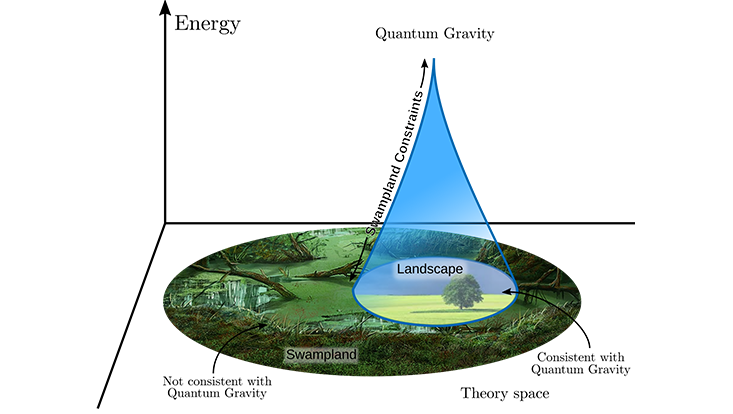
Photo: van Beest, Calderón-Infante, Mirfendereski, Valenzuela (2022)

Combining Quantum Mechanics and gravity into one theory is the theoretical challenge of the twenty-first century. The "Swampland Programme" aims to map out which models behave badly when coupled to gravity. One of the main expectations is the Swampland Distance Conjecture: travelling to extreme corners of parameter space causes certain models to run into trouble. Part of it was recently proved in holography by a collaboration between the Cluster of Excellence Quantum Universe and CERN.

The success of Quantum Mechanics, Special and General Relativity in the early twentieth century led to the elaboration of Quantum Field Theory (QFT) – a theory unifying Quantum Mechanics and Special Relativity into a single mathematical framework – which forms the basis for the Standard Model, our most complete understanding of particle physics. Although first hypothesized in the mid-1970, it was only fully experimentally verified in 2012 with the discovery of the Higgs boson. The greatest challenge of twenty-first-century high-energy physics has since been the quest for a theory of Quantum Gravity, where the principles of Quantum Mechanics are applied to spacetime itself. Unfortunately, the colossal energies needed make this task arduous, and current collider experiments cannot observe these Quantum-Gravity effects. Unlike the twentieth century, when experiments guided the Standard Model’s development, relevant experimental data may be decades away. What we do know, however, is that any correct theory must be mathematically consistent, an essential requirement that constrains the possible particles, their masses, and their interactions.

The Swampland Programme: Separating the Good From the Ugly

In Quantum Gravity, a model that satisfies all requirements of Quantum Field Theory may start behaving badly when gravity comes into play. One can then divide the set of all consistent QFT models into two: those that can be coupled to gravity, said to lie in the Landscape of Quantum Gravity, and those that cannot, which belong to the Swampland, as illustrated in the figure. In searching for a unified theory, it is crucial to uncover the properties that relegate certain models into the Swampland so they can be discarded. The better we understand these constraints, the more models can be ruled out, ideally leaving only a handful – or even unique! – candidates describing our universe. In recent years, theoretical physicists have posited a number of conjectures about the constraints imposed by Quantum Gravity, a line of research called the Swampland Programme. 

A central ingredient is the moduli space. It describes models that belong to a continuous family labelled by certain physical parameters like particle masses or the strength of interactions. These parameters are coordinates defining a specific model, like coordinates on a map point to a precise location. Just as distances can be measured between two points on Earth, distances can also be defined between models in moduli spaces.

The Swampland Distance Conjecture, one of the pillars of the Swampland Programme, then says that travelling large distances in a moduli space inevitably leads to an infinite tower of particles becoming light. At generic points, these particles are too massive to be detected by low-energy experiments and can be ignored and Quantum Field Theory works well. But at infinite distances they must be included in the model, violating a core principle of Quantum Field Theory: that the number of different particles is finite. The conjecture thus says that while Quantum Field Theory may approximate Quantum Gravity for some values of the parameters, at infinite distance the model breaks down and the full theory of Quantum Gravity is required. This conjecture has been shown to be true for large classes of models, although a complete proof remains elusive.

The AdS/CFT Correspondence: Two Facets of the Same Coin

One way to test these ideas is through the AdS/CFT correspondence, stating that Quantum Gravity on a specific spacetime, Anti-de Sitter (AdS) space, can be reformulated as a Conformal Field Theory (CFT), a special type of Quantum Field Theory invariant under angle-preserving transformations. In this so-called holographic picture, Quantum Gravity becomes “simpler” and can be expressed in the familiar QFT language, letting us recast the Swampland Programme into a simpler framework easier to study.

The moduli space of Quantum Gravity then corresponds to the space of deformations preserving conformal invariance. If the Swampland Distance Conjecture is true, something special must also occur when travelling infinite distances in that space. The equivalent to the Distance Conjecture states that only free theories can occur at infinite distance, meaning models with no interactions at all!

Proving Part of the CFT Distance Conjecture

By using CFT techniques, we proved part of the CFT Distance Conjecture: every free theory lies at infinite distance in the conformal manifold. Because free theories require specific numerical values for certain quantities, moving from any point in the space of deformations to a free theory must reproduce those values exactly. Using other consistency conditions we were led to the conclusion that free theories are always at infinite distance.

The greatest strength of our proof is its generality: it relies solely on generic features of Conformal Field Theory, not on additional symmetries or model-specific assumptions. This differs from other Swampland Programme studies, which often assume extra structures to retain computational control, but yield less universal results. By avoiding these model-dependent assumptions, our work reveals generic properties of Quantum Gravity in AdS. While our universe may not be AdS, it remains an important contribution to the broader effort of the Swampland Programme, its phenomenological consequences, and the quest for an updated Standard Model incorporating Quantum Gravity.

text by Florent Baume