Ambiguity in Self-dual Gauge Theory"Polarization Pairs" bring clarity

30 September 2025

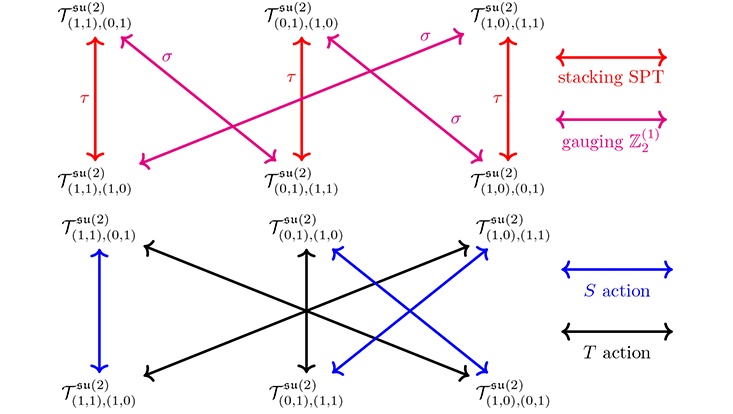
Photo: Craig Lawrie

For four-dimensional su(2) gauge theory, there are six polarization pairs, as depicted here. Different polarization pairs can be mapped into each other by physical process such as gauging a one-form symmetry, stacking an SPT phase, or acting with duality group transformations, as the different colored arrows show. Combinations of such transformations that start and end with the same polarization pair indicate that quantum field theory has a non-group-like symmetry.

A new framework introduces so-called polarization pairs as a datum necessary to have well-defined quantum field theories that involve self-dual gauge fields, in arbitrary even dimensions. This framework is a useful tool to reveal new types of symmetries in these theories – in particular those that go beyond traditional group-based structures.

Quantum field theory is a framework, originally developed to combine quantum mechanics with special relativity, which can be exploited to understand many phenomena in both physics and mathematics. One of the key properties of a quantum field theory, as in any physical system, are its symmetries.

In recent years, a refined notion of symmetry in quantum field theory has come to the fore. In the standard realization, a symmetry is defined by a mathematical structure known as a group, and a non-trivial action of the group on the local degrees of freedom of the theory in such a way that all physical observables are invariant under this action. This description suggests two generalizations: to define a symmetry via a more general mathematical structure, such as a so-called fusion category (sometimes referred to as capturing a “non-invertible” symmetry), and to allow a trivial action on the local degrees of freedom, but a non-trivial action on non-local degrees of freedom. A group-like symmetry that acts only on non-local degrees of freedom associated with a dimension k object is often called a k-form symmetry, analogously to the standard 0-form symmetry that acts on point-like degrees of freedom.

Quantum field theories often involve gauge fields, familiar from the photon in quantum electrodynamics, or the well-known SU(3) x SU(2) x U(1) gauge algebra of the Standard Model of Particle Physics. In four dimensions, these are 1-form fields, and for a quantum field theory in an arbitrary even number of dimensions (that is, a 2d-dimensional spacetime, for some d), they generalize to degrees of freedom captured by self-dual (d-1)-form fields. In general, a quantum field theory with such form fields is not well-defined: there exist physical questions, which in principle can be measured in an experiment, for which the theory does not predict a unique answer.

In the paper “Intermediate Defect Groups, Polarization Pairs, and Non-invertible Duality Defects”, Craig Lawrie, together with collaborators Xingyang Yu and Hao Zhang, propose a quantity, which they dub the polarization pair, which fully resolves this ambiguity in the definition of 2d-dimensional quantum field theories involving self-dual (d-1)-form gauge fields.

Given a particular set of (d-1)-form gauge fields, the authors explain how to determine the set of all possible polarization pairs, and once the pair has been specified, a (d-1)-form symmetry of the quantum field theory follows. Such a quantum field theory has a lattice of charged objects, and those lattices can themselves possess symmetries under which the charged objects are permuted. In fact, these transformations act naturally on the polarization pairs and can be thought of as providing a duality between theories specified by different polarization pairs. Using this formalism, the authors study how to combine these transformations of the charge lattice with the (d-1)-form symmetries to engineer quantum field theories with symmetries associated to fusion categories, instead of groups.

In this way, the authors show that it is vital to specify this novel mathematical object, the polarization pair, to have a well-defined quantum field theory with unambiguous answers to experiment questions, and furthermore that the polarization pair formalism allows one to determine the generalized symmetries of the quantum field theories, both higher-form symmetries and non-invertible symmetries.